💡 劝退指南
本文对一些统计学习方法原理进程了阐述,不可避免的引入了数学公式,有“数学恐惧”的同学可以跳过本文。
引言
几乎每个人都听说过机器学习,每个人也都有着自己的理解,我相信很多人的毕业论文跟机器学习密切相关,尤其是计算机相关的硕士同学。本文主要面向对机器学习的理解比较粗浅,想进一步加深认识的同学。
在与黑产斗智斗勇的过程中,我们也采用了机器学习的方法,比如在批量登录标签的产出中,我们使用了孤立森林;在注册数据的预测中,我们使用了时间序列自回归AR系列的模型。我们本次采用了较为简单好理解的线性回归,给大家做一个简单的讲解。
开始我们simple and easy的笔记旅程吧。
案例引入
所谓回归,我们都知道哈雷彗星大约75-76年就可以在地球上被肉眼观测到,在不久的2061年我们将能够再次见证他的回归。我们对哈雷彗星轨道和运行周期的准确预测其实就是回归的内涵。给定我们一组连续的输入变量,我们来预测一组连续的输出变量,这就是回归问题。
问题引入
那么接下来我们思考一下这个问题:
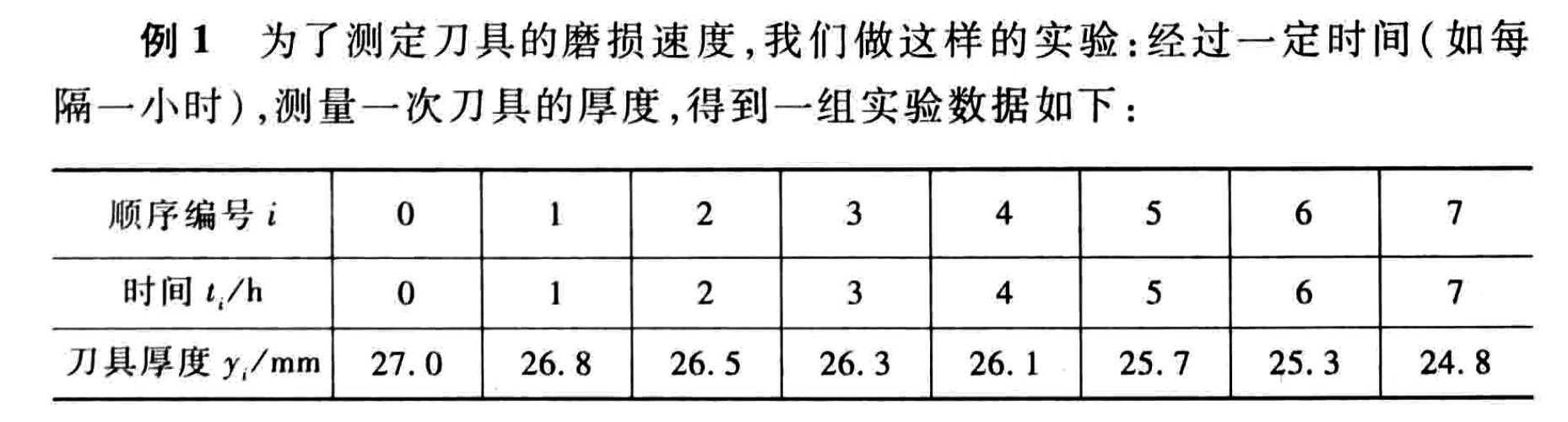
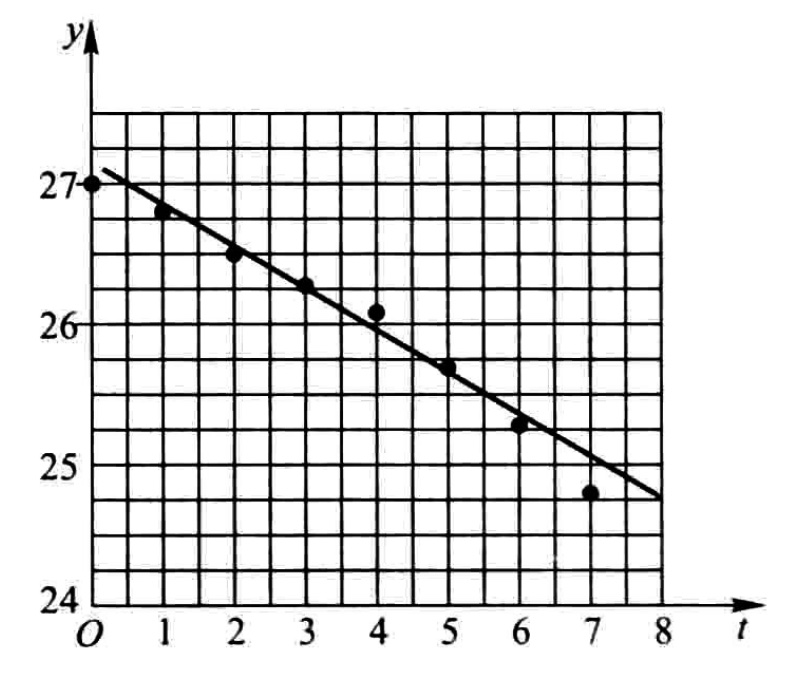
问题分析
这个问题需要确定刀具的磨损速度,是一个典型的回归问题。输入为时间和刀具厚度两个连续变量。从图中可以明显的看到,刀使用的时间越久,厚度就会越薄。美刀除外:)
💡 所谓连续变量:可以理解为两个值之间可以无限分割,如人的身高
💡 所谓离散变量:可以理解某几种分类,比如投骰子,只有1~6,没有1.1
这种越xx越yy的问题,我们可以理解为有正相关或负相关,比如说买房的人越多,房价越高;大盘越绿,天台上人越多;
从图中我们可以看到,时间与刀具厚度的关系的描点,大致上接近于一条直线。于是,我们可以认为它是线性的。
到了这里,那不就是个曲线(直线)拟合问题吗?嗨,这谁不会啊?
问题解答
直线的函数相信大家已经很熟悉了,二元一次方程嘛。已知时间t和刀具厚度y,我们可设:
\[y = at + b\]
那么其中的常数a和b如何确定呢?理想情况下,我们的直线\(y = at + b\)可以经过图中所标出的各点,但实际上这显然不可能!因为这些点根本就不在一条直线上!

那么我们只能退而求其次,选择一条直线,使得这条直线与这些点尽量的离得近。
所以到这里,问题就变成了,要找到一条跟图中的点偏差最小的直线,也就是求得a和b即可。
表格中一共8组数据
时间:\(t_{0},t_{1},t_{2},...,t_{7}\)
刀具厚度:\(y_{0},y_{1},y_{2},…,y_{7}\)
如果我们要让直线的偏差尽量的小,那么就等价于在直线\(y = at + b\)上\(t_{0},t_{1},t_{2},...,t_{7}\)处的函数值与刀具厚度数据\(y_{0},y_{1},y_{2},…,y_{7}\)相差都很小, 即每个点X都要小
\[X_{i} = y_{i} - (at_{i} + b)\]
极值求解
那么怎么让每个X都很小呢?
如果X的和加起来很小是不是每个X都很小了呢?

不的。
因为偏差有正有负,在求和时,可能互相抵消,为了避免这种情况,可以先对偏差取绝对值再求和。
\[\sum_{i = 0}^{7} |y_{i} - (at_{i}+b)|\]
但是绝对值也不是特别好算,我们取个平方。
\[M=\sum_{i=0}^{7}[y_{i} - (at_{i}+b)]^2\]
我们这里要取最小值,并且用到了平方,所以这种方法就叫“最小平方法(least squares method)”,当然啦“最小二乘法”是更常见的称呼。它专门用来确定常数a和b。
那么现在,我们就要确定a和b符合什么条件时,可以使上面公式中的M最小。
学过高等数学的人都知道,这不就是一个多元函数求极值的问题嘛!
怎么求极值,求偏导,然后偏导为0,解方程就行了。来让我们手动求一遍。
定理1(必要条件)
设函数\(z=f(x, y)\)在点\((x_{0}, y_{0})\)具有偏导数,且在点\((x_{0}, y_{0})\)处有极值,则有
\[f_{x}(x_{0}, y_{0}) = 0, f_{y}(x_{0}, y_{0}) = 0\]
根据定理1,我们有
\[\begin{cases} M_{a}(a,b) = 0, \\ M_{b}(a,b) = 0. \end{cases}\]
然后我们对M公式求偏导可得,
\[ \left\{\begin{matrix} \frac{\mathrm{\partial \mathit{M} }}{\partial \mathit{a}} = -2 \sum_{i-0}^{7} [y_{i} - (at_{i} + b)]t_{i} = 0, \\ \frac{\mathrm{\partial \mathit{M} }}{\partial \mathit{b}} = -2 \sum_{i-0}^{7} [y_{i} - (at_{i} + b)] = 0. \end{matrix}\right. \]
即
\[ \left\{\begin{matrix} \sum_{i-0}^{7} [y_{i} - (at_{i} + b)]t_{i} = 0, \\ \sum_{i-0}^{7} [y_{i} - (at_{i} + b)] = 0. \end{matrix}\right. \]
将括号内各项进行整理合并,并把未知数a和b分离出来,得
\[ \left\{\begin{matrix} a\sum_{i-0}^{7}t_{i}^2 + b\sum_{i-0}^{7}t_{i} = \sum_{i-0}^{7}y_{i}t_{i}, \\ a\sum_{i-0}^{7}t_{i} + 8b = \sum_{i-0}^{7}y_{i}. \end{matrix}\right. \]
下面通过列表来计算\(\sum_{i-0}^{7}t_{i}, \sum_{i-0}^{7}t_{i}^2, \sum_{i-0}^{7}y_{i}, \sum_{i-0}^{7}y_{i}t_{i}\)
| \[t_{i}\] | \[t_{i}^2\] | \[y_{i}\] | \[y_{i}t_{i}\] | |
|---|---|---|---|---|
| 0 | 0 | 27.0 | 0 | |
| 1 | 1 | 26.8 | 26.8 | |
| 2 | 4 | 26.5 | 53.0 | |
| 3 | 9 | 26.3 | 78.9 | |
| 4 | 16 | 26.1 | 104.4 | |
| 5 | 25 | 25.7 | 128.5 | |
| 6 | 36 | 25.3 | 151.8 | |
| 7 | 49 | 24.8 | 173.6 | |
| \[\sum\] | 28 | 140 | 208.5 | 717.0 |
带入上述方程组,得到
\[\left\{\begin{matrix} 140a + 28b = 717, \\ 28a + 8b = 208.5. \end{matrix}\right.\]
解方程组,得到a=-0.3036,b=27.125
这样便得到刀具的磨损速度函数,\[y = -0.3036t + 27.125\]
看到这里我们知道了什么是最小二乘法,它解决了刀具磨损速率的问题,并且在衡量偏差最小的方案中,认为绝对值和平方都是可行的。其实,在机器学习中,我们都听说过一个概念:损失函数。对于我们这个问题而言,M如果等于0,则我们认为没有损失,如果M不等于0则认为是我们在计算回归函数的时候,是存在损失的。损失函数越小,意味着我们选取的方法就也就越好。
但是损失函数的之间也是有差别的,绝对值损失函数与平方损失函数都是非常常见的损失函数。对于我们这个场景来说,都可以适用。
那么还有没有其他方法能解决这个问题呢?
梯度下降法
从上面我们知道,问题的关键就在于要求出一个a和b使得M的值最小,也就是一个求解最小值的问题。
在机器学习中,对于求解最优化问题,梯度下降法是一种最常用的办法。
那么什么是梯度下降呢?
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
这句话其实不难理解,所谓的梯度是针对多元函数而言的,那么对于一元函数来说,其实就是导数。
比如,我们都熟悉下面的这个一元二次方程
\[f(x) = x^{2} - 10x + 1\]
如果我们要求其极值,当其导数为0时,\(f(x)\)有极值。
\[{f}'(x) = 2x - 10 \]
显然,当x=5时,f(x)有极小值。
对于多元函数来说,像上面这种直接通过求导就能得到唯一解的理想情况并不太多,所以就有了通过找近似解的方式去逼近极值,也就是通过梯度下降法。梯度是有方向的,梯度的方向是局部最大的方向,所以梯度下降就是往梯度的反方向求局部最小值,也就是去找损失函数的最小值。
当我们看到逼近的时候,就以为这会有迭代,不断迭代求得极值,那么梯度下降是如何通多迭代求得极值的呢?
梯度下降公式及推导
我们不妨看看梯度下降的公式:
\[x = x_{0} - \eta \cdot \nabla f(x_{0})\]
其中\(x\)是自变量的下一个位置,\(x_{0}\)是自变量当前位置,\(\eta\)是步长(标量,一般为正值),\(\nabla f(x_{0})\)是梯度值,\(-\)代表梯度下降方向。
我们要求解\(f(x)\)的极小值,\(f(x)\)需满足具有一阶连续偏导数,我们对\(f(x)\)在\(x_{0}\)处进行一阶泰勒展开。
\[f(x) = f(x_{0}) + (x -x_{0})\nabla f(x_{0})\]
其中\(x - x_{0}\)是向量,\(x - x_{0}\)的单位向量用\(v\)标识,我们令:
\[x - x_{0} = \eta v\]
带入上述方程可得
\[f(x) = f(x_{0}) + \eta v \nabla f(x_{0})\]
理想情况是,\(x\)每次更新都能让\(f(x)\)变小,即
\[f(x) - f(x_{0}) = \eta v \nabla f(x_{0}) < 0\]
即
\[v \nabla f(x_{0}) < 0\]
\(v\)和\(\nabla f(x_{0})\)都是向量,\(\nabla f(x_{0})\)为当前梯度方向,当\(v\)与当前梯度方向相反的时候,\(v \nabla f(x_{0})\)能够最小,也就保证了v的方向是局部下降最快的方向。因为\(v\)是单位向量,所以有,
\[v = - \frac{\nabla f(x_{0})}{|| \nabla f(x_{0}) ||}\]
将其带入到\(x - x_{0} = \eta v\)中,
\[x - x_{0} = - \eta \frac{\nabla f(x_{0})}{|| \nabla f(x_{0}) ||}\]
\(|| \nabla f(x_{0}) ||\)是标量,我们将其合并到\(\eta\)中,得到
\[x = x_{0} - \eta \cdot \nabla f(x_{0})\]
即梯度下降的公式。
用梯度下降的方法解决问题
我们回到刀具磨损的问题上来。
我们定义一个绝对值损失函数 \(X_{i} = |y_{i} - (at_{i} + b)|\)
然后进行计算。
未完待续。
机器学习的分类
- 监督学习的本质是学习输入到输出的映射的统计规律。
- 无监督学习的本质是学习数据中的统计规律或潜在结构。
- 强化学习本质是学习最优的序贯决策。
参考文档
- 高等数学