正则化的概念
模型选择的典型方法是正则化(regularization)。正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或罚项(penalty term)。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。
正则化一般具有如下形式:
\[\min_{f\in \mathcal{F}} \frac{1}{N} \sum_{i=1}^{N}L(y_{i},f(x_{i})) + \lambda J(f)\]
其中,第一项是经验风险,第2项是正则化项,\(\lambda \ge 0\) 为调整两者之间关系的系数。
简单来说,正则化是为了解决过拟合问题,增强泛化能力。
过拟合
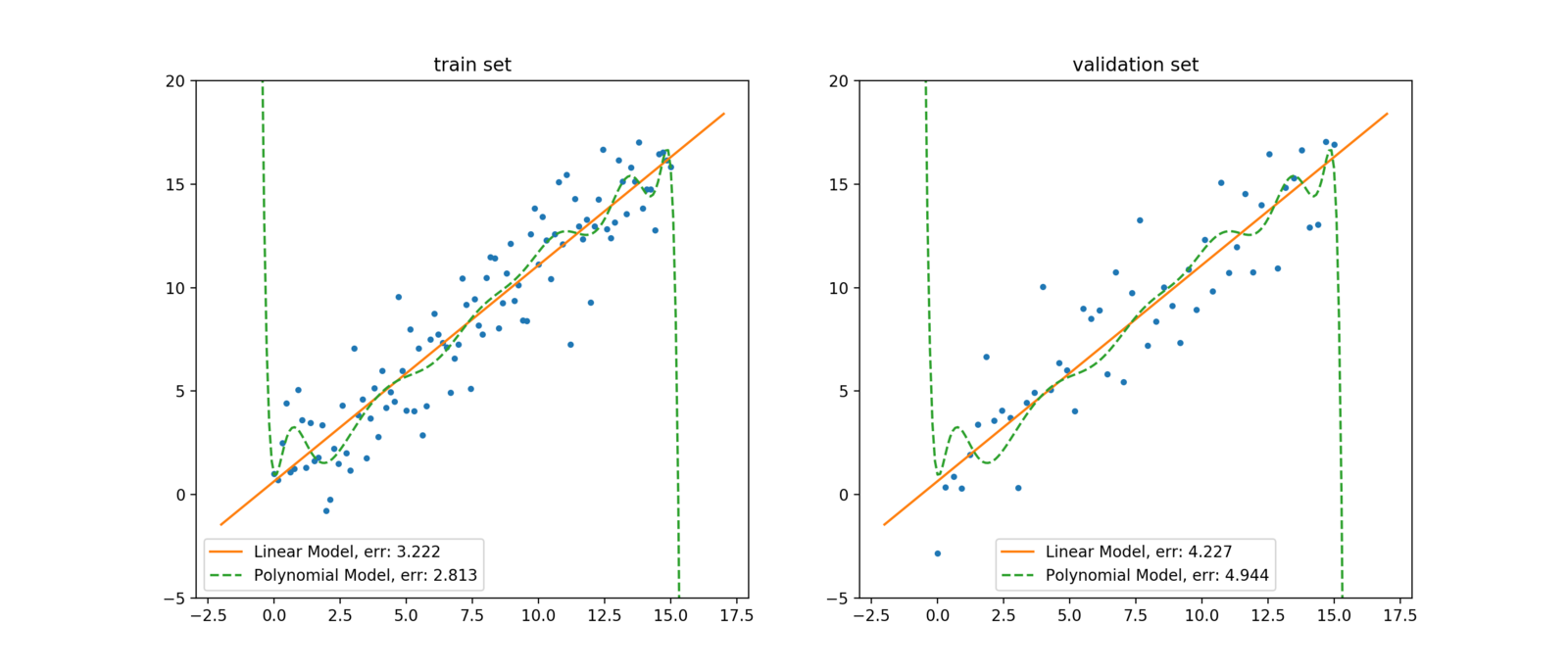
图中左侧是训练集,右侧是验证集。训练集和验证集数据均是由线性函数加上一定的随机扰动生成的。图中橙色直线是以线性模型拟合训练集数据得到模型的函数曲线;绿色虚线则是以15-阶多项式模型拟合训练数据得到模型的函数曲线。由此可见,尽管多项式模型在训练集上的误差小于线性模型,但在验证集上的误差则显著大于线性模型。此外,多项式模型为了拟合噪声点,在噪声点附近进行了高曲率的弯折。这说明多项式模型过拟合了训练集数据。
正则化的作用
- L1正则化可以使得参数稀疏化,即得到的参数是一个稀疏矩阵,可以用于特征选择;
- L2正则化可以防止模型过拟合(overfitting);
\(L_{1}\)正则化
机器学习模型当中的参数,可形式化地组成参数向量,记\(\vec{\omega} \)。不失一般性,以线性模型为例:
\[F(\vec{x} ; \vec{\omega}):=\vec{\omega}^{\top} \cdot \vec{x}=\sum_{i=1}^{n} \omega_{i} \cdot x_{i}\]
由于训练集当中统计噪声的存在,冗余的特征可能成为过拟合的一种来源。这是因为,对于统计噪声,模型无法从有效特征当中提取信息进行拟合,故而会转向冗余特征。为了对抗此类过拟合现象,人们会希望让尽可能多的\(\omega_{i}\)为零。为此,最直观地,可以引入\(L_{0}\)*-正则项
\[\Omega(F(\vec{x} ; \vec{\omega})):=\gamma_{0} \frac{|\vec{\omega}|{0}}{n}, \gamma{0}>0\].
通过引入\(L_{0}\)-正则项,人们实际上是向优化过程引入了一种惩罚机制:当优化算法希望增加模型复杂度(此处特指将原来为零的参\(\omega_{i}\)更新为非零的情形)以降低模型的经验风险(即降低全局损失)时,在结构风险上进行大小为 \(\frac {\gamma_{0}}{n}\)的惩罚。于是,当增加模型复杂度在经验风险上的收益不足\(\frac {\gamma_{0}}{n}\)时,整个结构风险实际上会增大而非减小。因此优化算法会拒绝此类更新。
引入\(L_{0}\)-正则项可使模型参数稀疏化,以及使得模型易于解释。但\(L_{0}\)-正则项也有无法避免的问题:非连续、非凸、不可微。因此,在引入\(L_{0}\)-正则项的目标函数上做最优化求解,是一个无法在多项式时间内完成的问题。于是,人们转而考虑\(L_{0}\)-范数的最紧凸放松——\(L_{1}\)-范数,令
\[\Omega(F(\vec{x} ; \vec{\omega})):=\gamma_{1} \frac{|\vec{\omega}|{1}}{n}, \gamma{1}>0\].
和引\(L_{0}\)-正则项的情况类似,引\(L_{1}\)-正则项是在结构风险上进行大小为\(\frac{\gamma_{1}|\omega_{i}|}{n}\)的惩罚,以达到稀疏化的目的。
\(L_{2}\)正则化
在发生过拟合时,模型的函数曲线往往会发生剧烈的弯折,这意味着模型函数在局部的切线之斜率非常高。一般地,函数的曲率是函数参数的线性组合或非线性组合。为了对抗此类过拟合,人们会希望使得这些参数的值相对稠密且均匀地集中在零附近。于是,人们引入了\(L_{2}\)-范数,作为\(L_{2}\)-正则项。令
\[\Omega(F(\vec{x} ; \vec{w})):=\gamma_{2} \frac{|\vec{\omega}|{2}^{2}}{2 n}, \gamma{2}>0\]
于是有目标函数
\[Obj(F)=L(F)+\gamma_{2} \frac{|\vec{\omega}|_{2}^{2}}{2 n}\]
于是对于参数\(\omega_{i}\)取偏微分
\[\frac{\partial \mathrm{Obj}}{\partial \omega_{i}}=\frac{\partial L}{\partial \omega_{i}}+\frac{\gamma_{2}}{n} \omega_{i}\]
因此,在梯度下降时,参数\(\omega_{i}\)的更新
\[\omega_{i}^{\prime} \leftarrow \omega_{i}-\eta \frac{\partial L}{\partial \omega_{i}}-\eta \frac{\gamma_{2}}{n} \omega_{i}=\left(1-\eta \frac{\gamma_{2}}{n}\right) \omega_{i}-\eta \frac{\partial L}{\partial \omega_{i}}\]
注意到\(\eta \frac{\gamma_{2}}{n}\)通常是介于(0,1)之间的数,\(L_{2}\)-正则项会使得参数接近零,从而对抗过拟合。