梯度下降公式
$$\theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)$$
线性回归函数
$$h_{\theta} = \theta_{0} + \theta_{0}x$$
线性回归损失函数
$$J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}(x^{(i)})-y^{(i)}\right)^{2}$$
即: $$J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\theta_{0} + \theta_{1}x^{(i)}-y^{(i)}\right)^{2}$$
对损失函数求偏导数(见图片)
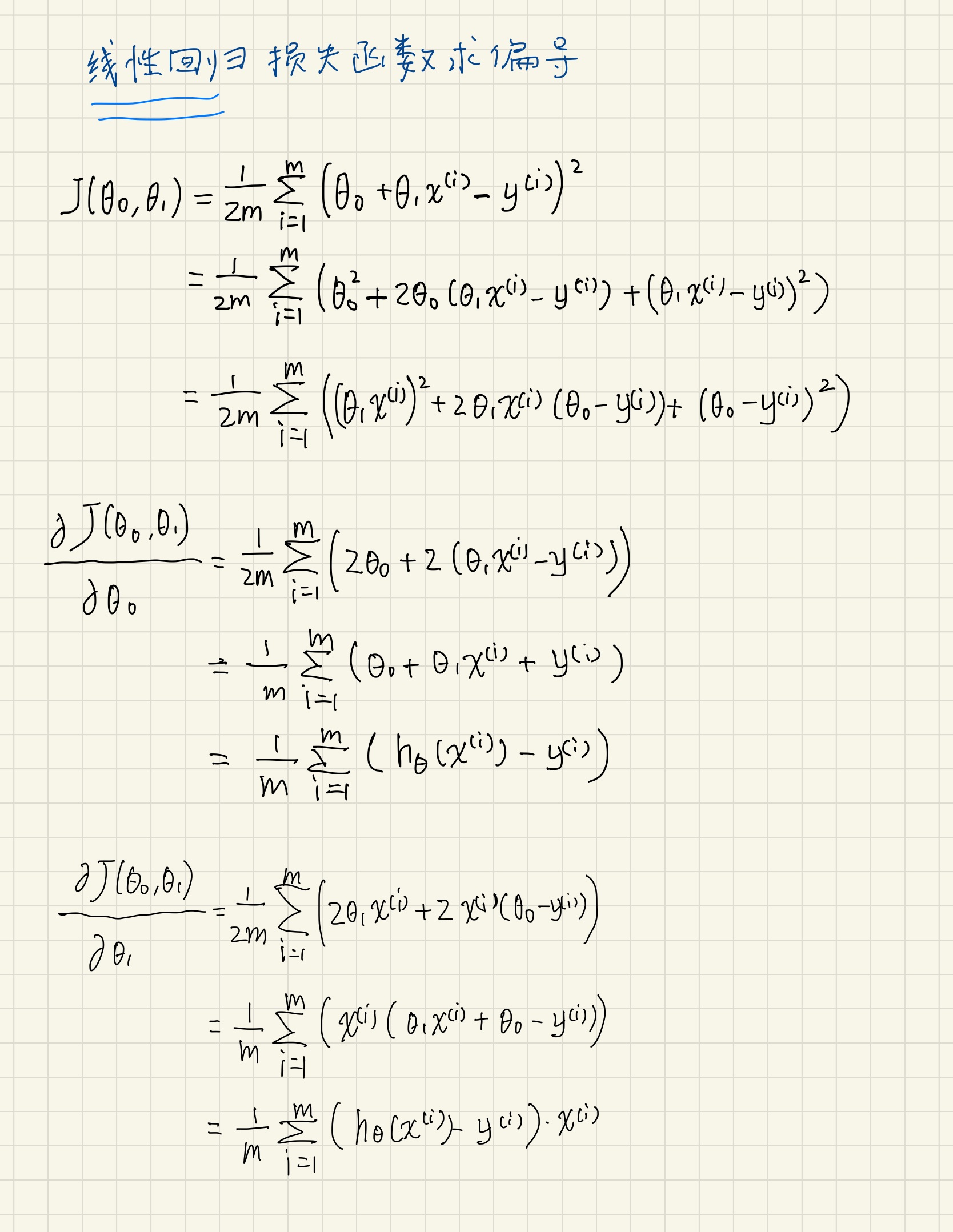
将结果带入梯度下降公式
$$\theta_{0}:=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m} \left(h_{\theta}(x^{(i)})-y^{(i)}\right) $$
$$\theta_{1}:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m} \left((h_{\theta}(x^{(i)})-y^{(i)}) \cdot x^{(i)}\right)$$